The Empirical Potential Energy Function

Each of the interactions commonly employed in the potential energy function $V(\vec{R})$ is sketched below. Simple harmonic terms describe bond stretching and angle bending. The planarity of groups (e.g., the amide planes of proteins) can also be enforced by harmonic potentials known as an improper dihedrals. Rotation about single bonds (torsions) is governed by sinusoidal energies.

The electrostatic attraction or repulsion between two charges is described by Coulomb's law:

$$V_{ij}^{Coulomb}(r_{ij}) = \frac{q_i q_j}{4 \pi \epsilon_r \epsilon_0 r_{ij}},$$

where $q_i$ and $q_j$ are the atoms' partial charges, $r_{ij}$ is the distance separating the atoms' centers, $\epsilon_0$ is the permittivity of free space, and $\epsilon_r$ is the relative dielectric coefficient of the medium between the charges (i.e., $\epsilon_{medium} = \epsilon_r \epsilon_0$).

A distance-dependent dielectric coefficient (RDIE: $\epsilon_r = r_{ij}$) has been used to approximate solvent screening without including explicit water molecules. Physically, it's a pretty ugly way to cheat. But if you don't want to include water, it may be the best your simulation package has to offer; it is almost certainly better than using unscreened partial charges in the absence of water. For realistic dynamics, we recommend constant-dielectric (CDIE) simulations with explicit solvation and $\epsilon_r = 1$. The presence of water retards conformational searching, however.

An important electrodynamic effect remains to be included: van der Waals interactions. The electron cloud of a neutral atom fluctuates about the positively charged nucleus. The fluctuations in neighboring atoms become correlated, inducing attractive dipole-dipole interactions. The equilibrium distance between two proximal atomic centers is determined by a trade off between this attractive dispersion force and a core-repulsion force that reflects electrostatic repulsion and the Pauli exclusion principle. The Lennard-Jones potential models the attractive interaction as $\propto r_{ij}^{-6}$ and the repulsive one as $\propto r_{ij}^{-12}$:

$$V_{ij}^{LJ}(r_{ij}) = \varepsilon_{ij} \left[ \left( \frac{r... ...{12} - 2 \left( \frac{r_{ij}^{min}}{r_{ij}} \right)^6 \right],$$

where $r_{ij}^{min}$ is the equilibrium separation distance (where the force $F = -dV_{ij}^{LJ}/dr_{ij} = 0$) and $\varepsilon_{ij}$ is the well depth; i.e., $V_{ij}^{LJ}(r_{ij}^{min}) = -\varepsilon_{ij}$. Why this `6-12' form for the van der Waals interaction? The application of quantum perturbation theory to two well separated hydrogen atoms in their ground states yields an interaction energy that decays as $r_{ij}^{-6}$, and $r_{ij}^{-12}$ is obviously easy to calculate from $r_{ij}^{-6}$. For simplicity, the Lennard-Jones forces are typically modeled as effectively pair-wise additive: the potential energy $V_{ABC}$ of three adjacent particles A, B, and C is the sum of the three energies for each atom pair: $V_{ABC} = V_{AB} + V_{BC} + V_{AC}$. Pair-wise additivity is only an approximation.

Perhaps, you are thinking, `Hey, what about magnetic forces?' The magnetic force between two moving charges is expressed in terms of a double vector cross product involving the two particle velocities and the vector $\vec{r}_{ij}$ of separation. It does not generally act along $\vec{r}_{ij}$, but it does when two charges q have instantaneous velocities v along parallel lines. For this case, we can conveniently compare the magnitudes of the magnetic and electric forces. It turns out that the magnetic force is weaker than the electric force by a factor of $(v/c)^2$, where c is the speed of light. Thus, magnetic forces are neglible for nonrelativistic particles, such as the partial charges that are used in simulation force fields. For example, if a particle moves as much as 1 Å in as short a time as 1 femtosecond ($10^{-15}$ s), then $(v/c)^2 = 1.1 * 10^{-7}$. We may therefore completely neglect magnetic interactions.

Interactions included in representative potential energy function
for MD simulation.

For those who like equations with their pictures, a typical potential energy function used in MD simulations looks like:

$$V(\vec{R}) = V_{bonded}(\vec{R}) + V_{nonbonded}(\vec{R}),$$

with

$$V_{bonded}(\vec{R}) = \sum_{bonds} k_l (l - l_0)^2 + \sum_{a... ...^2+ \sum_{torsions} A_n \left[ 1 + cos(n\phi - \phi_0) \right]$$

$$V_{nonbonded}(\vec{R}) = \sum_{i<j} \left( \varepsilon_{ij} ... ... \frac{q_i q_j} { 4 \pi \epsilon_r \epsilon_0 r_{ij} } \right)$$

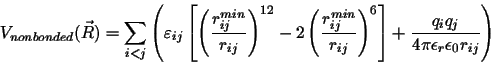
The first `bonded' sum is over bonds between atom pairs; the second sum is over bond angles defined by three atoms; the third and fourth sums are over atom foursomes (as in the figure above). For bookkeeping purposes, each atom is assigned a number. In the `nonbonded' interactions (van der Waals and electrostatics), the summation is over atoms i and j, where `i < j' simply ensures that each interaction is counted only once. Generally, atoms separated by one or two bonds are excluded from the nonbonded sum, and those separated by three bonds, `1-4 interactions', may have electrostatic interactions reduced by a multiplicative scale factor. The form of $V(\vec{R})$ shown here reflects the choice not to include an explicit hydrogen bond term, favoring instead to account for hydrogen bonds through an appropriate parameterization of Lennard-Jones and Coulomb interactions. Note also that a single dihedral angle (torsion) may have an energy described by more than one Fourier component (multiple values of n).