§18.21 Hahn Class: Interrelations
Contents
§18.21(i) Dualities
¶ Duality of Hahn and Dual Hahn
18.21.1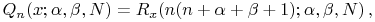
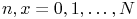 .
.
For the dual Hahn polynomial ![]() see
§18.25.
see
§18.25.
¶ Self-Dualities
18.21.2
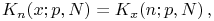
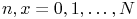 .
.

 .
.

 .
.
§18.21(ii) Limit Relations and Special Cases
¶ Hahn  Krawtchouk
Krawtchouk
18.21.3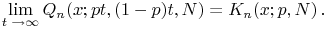
¶ Hahn  Meixner
Meixner
18.21.4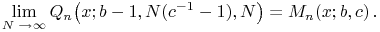
¶ Hahn  Jacobi
Jacobi
18.21.5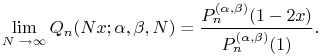
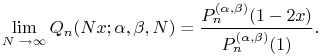
¶ Krawtchouk  Charlier
Charlier
18.21.6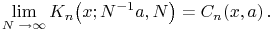
¶ Meixner  Charlier
Charlier
18.21.7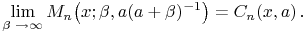
¶ Meixner  Laguerre
Laguerre
18.21.8

¶ Charlier  Hermite
Hermite
18.21.9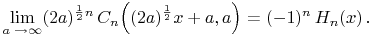
¶ Continuous Hahn  Meixner–Pollaczek
Meixner–Pollaczek
18.21.10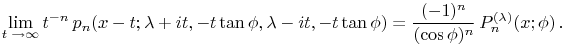
18.21.11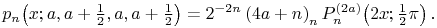
¶ Meixner–Pollaczek  Laguerre
Laguerre
18.21.12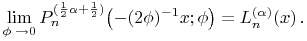
A graphical representation of limits in §§18.7(iii), 18.21(ii), and 18.26(ii) is provided by the Askey scheme depicted in Figure 18.21.1.
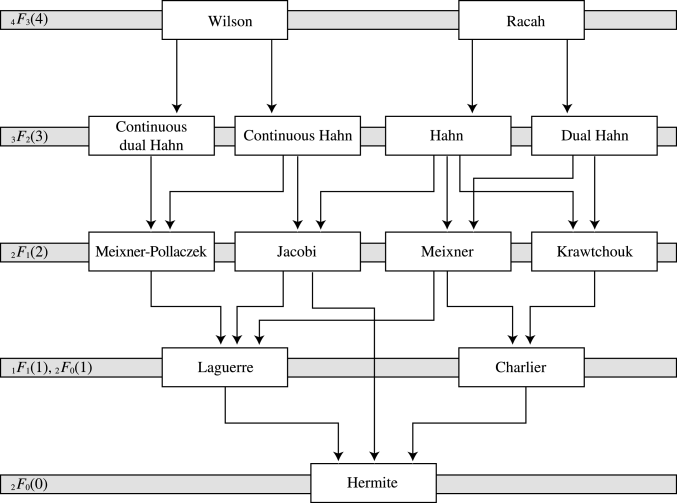
Figure 18.21.1: Askey scheme. The number of free real parameters is zero for Hermite
polynomials. It increases by one for each row ascended in the scheme,
culminating with four free real parameters for the Wilson and Racah
polynomials. (This is with the convention that the real and imaginary
parts of the parameters are counted separately in the case of the
continuous Hahn polynomials.)



